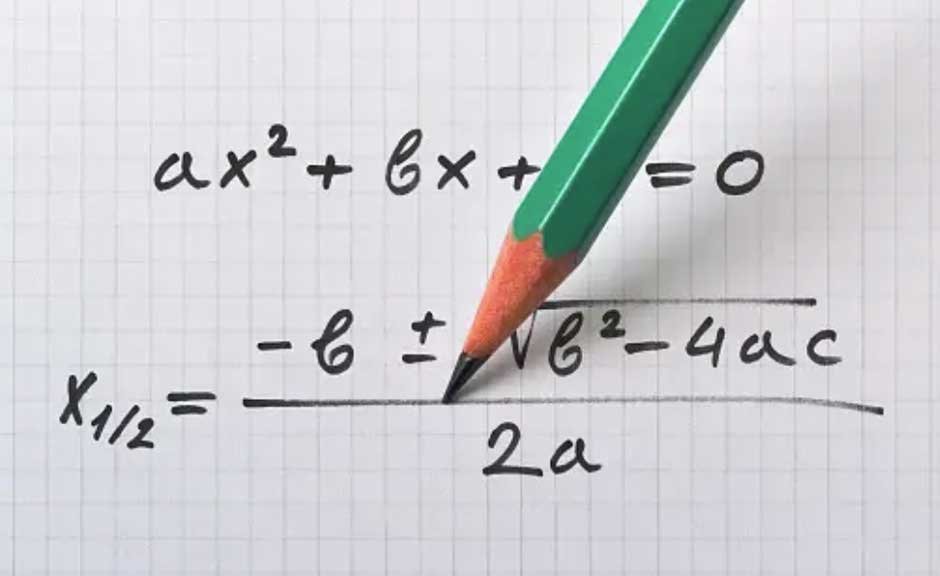A polynomial equation in one variable with a maximum exponent of two is called a quadratic equation. Quadratic equations can be solved in three different methods: To utilize the quadratic formula, To factor the quadratic equation if possible, or To finish the square. Simply follow these steps to learn how to master these three techniques.
Calculating the Equation’s Factor
Move all like terms to one side of the equation and combine them. Moving every term to one side of the equation while maintaining the positive value of the ⁰ 2 x^{2} term is the initial step in factoring an equation. Add or subtract all of the x terms, y terms, and constants (integer terms) to one side of the equation so that nothing is left on the other to combine the terms. You can just write “0” on that side of the equal sign after there are no more terms on that side. Use formulas for Quadratic equation root finder.
- Divide the expression into factors. You must use the factors of the ⁰ 2 to factor the expression. The middle term (-11) is obtained by multiplying the x^{2} term (3) by the factors of the constant term (-4). This is the way to accomplish it:
- The factors 3⁽ 3x and 3⁽ x are the only viable factors for 3⁽ 2 3x^{2}, thus you may put them in parenthesis: (·3ᅵ ± ? ) ( ± ? ) = 0 (3x\pm?)(x\pm?)=0.
- Next, enter the factors of 4 using the process of elimination to identify a combination that, when multiplied, yields -11x. Since both numbers multiply to provide 4, you can either employ a combination of 4 and 1 or 2 and 2. Just keep in mind that since the word is -4, one of the terms needs to be negative.[3]
- Try varying this combination of elements (3⁰ + 1)(⁰ − 4)(3x+1)(x-4), by trial and error. The result of multiplying them out is 3 ⁽ 2 − 12 ⁽ + ⁽ − 4 3x^{2}-12x+x-4. You can obtain the middle word you were seeking, − 11 11x, by combining the terms − 12 12x and ⁰ x. Just now, the quadratic equation was factored in.
- As a trial-and-error exercise, let’s see if we can verify a factoring combination for 3x^{2}-11x-4=0 3x¿2}-11x-4=0 That is incorrect and inoperable:
- ( 3 ⁰ − 2) ( ⁰ + 2) (3x-2)(x+2) = 3 ⁽ 2 + 6 ⁽ − 2 ⁽ − 4 3x^{2}+6x-2x-4. Upon combining those terms, you obtain 3 ⁽ 2 − 4 ⁽ − 4 3x^{2}-4x-4. Even if elements -2 and 2 multiply to get -4, the middle term is not valid because you required − 11x⁽-11x, not − 4x⁰-4x.
Set the Equation
Put a zero in each parenthesis as a separate equation. This will lead you to determine the two values of x that will cause the total equation, ( 3 ⁜ + 1) ( ⁰ − 4) ( 3x+1)(x-4) = 0, to equal zero. All that’s left to do is factor the equation and set the expression in each set of parenthesis to equal zero. However, why? Since the “principle, rule, or property” states that one element must equal zero for multiplication to result in zero, at least one of the factors in parenthesis, such as (3x+1)(⁰−4)(3x+1)(x-4) must equal zero; that is, either (3x + 1) or else (x – 4) must equal zero. Thus, you would write 3 ⁰ + 1 = 0 3x+1=0 as well as ⁰ − 4 = 0 x-4=0.
Solving the Quadratic Equations
- Put every term on one side of the calculation. Verify if the phrase an or x2 is positive. The method is as follows.
- 12x – 9 – 2×2 = 0
The a, b, and c terms in this equation are 2 -12, and -9, respectively.
- Transfer the constant or c-word to the opposite side. The numerical term devoid of a variable is called a constant term. Transfer it to the equation’s right side.
- Divide each side by the an or x2 term’s coefficient. You can skip this step if x2 merely has a coefficient of 1 and no terms in front of it. In this instance, you will need to split each term by two.
- After simplifying the radical, find x. Find a perfect square within the numbers 27 or 2, or in their factors, to simplify ±√(27/2). Since 9 x 3 = 27, the perfect square 9 can be found in 27. Remove the number 9 from the radical sign by pulling it out and writing the square root of 9—3, outside the radical sign. Since the factor of 27 cannot be removed, leave 3 in the numerator of the fraction under the radical sign and leave 2 at the bottom. After that, write down your two answers for x and transfer the constant 3 from the left side of the equation to the right. Quadratic equations can’t be used for Percentage Average Finder.
Conclusion
If your expression has two roots, it is a perfect square. It also implies that there is no discrimination. You can solve the equation in k that results from using either of these to find the solution. The formula for a square is (ax+b)^2= a^2 x^2 + 2abx + b^2. Since b = +1 or -1, it follows naturally that a=+/-(k+1)/2 = sqrt(k+4).